I attended the Wolfram Summer School 2020 this summer. A total of 80 students were selected from all over the world after applications and interviews. Owing to the Coronavirus lockdown, it was organised in a virtual manner this time. Due to this, I experienced a “virtual jet lag” for the first few days as the time zones of the School (EDT) was completely opposite to my home town (Delhi) timezone. Keeping aside this technical aspect, the School was a wonderful experience. Wolfram Language training sessions were held on various interesting topics like audio and video manipulation, graphs and networks, machine learning and neural networks. There were interactive sessions with Stephen Wolfram himself! It was indeed quite inspiring to learn about his life and “virtually” visit his home.

My project during the School was on running “Cellular Automata (CA) on 3D Lattices.” Here is the abstract of the project from the Wolfram Community Post I published on the Wolfram Community Blog:

The aim of the project is to work with lattices (in 3D) and to be able to perform computational tasks on the lattice elements. This requires proper indexing of the lattice points themselves, as well as the unit cells defined on them (by the basis vectors). A nice way to visualise the computation (and to check if the indexing is proper) is to be able to run Cellular Automaton on the lattices and plot the output state by highlighting the unit cells or the lattice points which have the desired state (a state of “1” as a result of the Cellular Automaton). The indexing of lattice points and unit cells would enable us to create a 3D analogue of the 2D ArrayPlot function. Finally, the neighbourhoods of the lattices are classified which is crucial for defining Cellular Automata rules. The Cellular Automata would yield interesting patterns within the lattice and provide models for crystal growth.

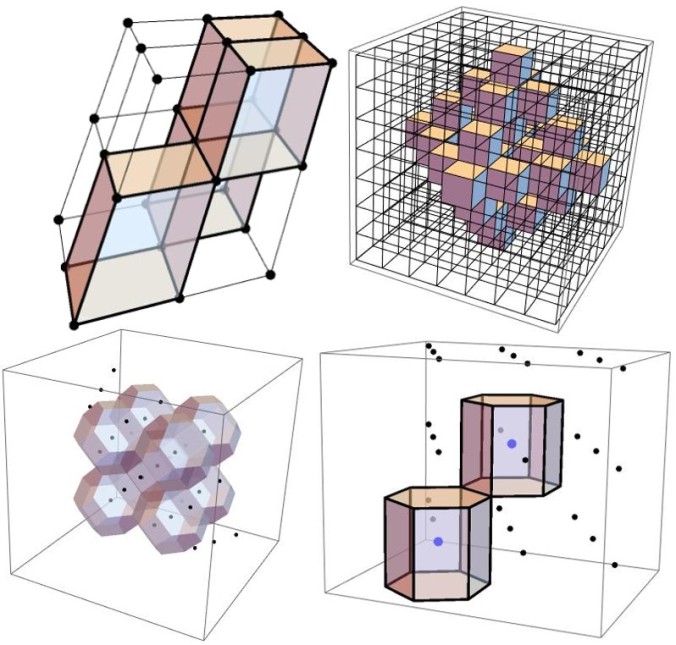
Some interesting images from the result of my work

When it comes to running CA on 3D lattices, there are two ways of working:

  1. Unit Cells
  2. Lattice Points

The unit cell defined from a set of three basis vectors would be a parallelepiped, whose neighbourhood structure is similar to that of a cube. Interesting shapes arise when working with lattice points. In this case, one has to work with the Voronoi regions around the lattice points. All the fourteen Bravais lattices could be grouped into five Voronoi types, given below.

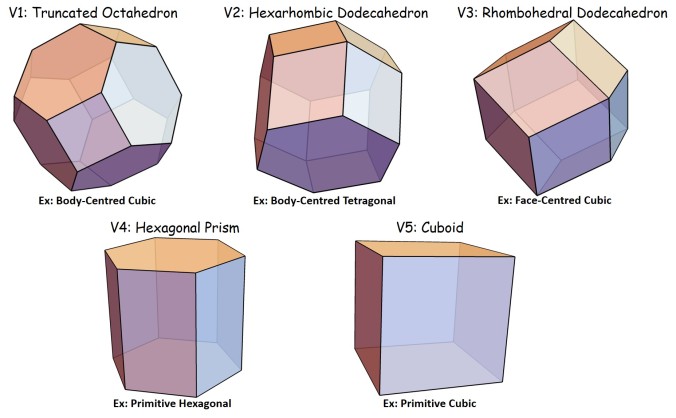
Visit my Wolfram Community Post published on the Wolfram Community Blog to know the results upon running a few CA on these shapes. To get a glimpse a general overview of the work, visit my YouTube video.